Graph and Graph Representations

A graph is a data structure that consists of a finite set of vertices or nodes, and a set of edges connecting these vertices. The vertices and edges together form the graph. Graphs can be used to model a wide range of relationships or connections between objects.

Basic Components:

Vertex (or Node): It represents an entity in the graph.

Edge: It represents a connection or relationship between two vertices.

Types of Graphs:

Directed Graph (Digraph): In a directed graph, edges have a direction. The edge from vertex A to vertex B is different from the edge from B to A.

Undirected Graph: In an undirected graph, edges do not have a direction. The edge connecting vertex A to vertex B is the same as the edge connecting B to A.

Weighted Graph: Each edge in the graph has an associated weight or cost.

Cyclic Graph: A graph that contains at least one cycle (a path that starts and ends at the same vertex).

Acyclic Graph: A graph that does not contain any cycles.

Graph is a mathematical structures used to model relations between objects from a certain collection. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges. Typically, a graph is depicted in diagrammatic form as a set of circles for the vertices, joined by lines or curves for the edges graph may be undirected(a), meaning that there is no distinction between the two vertices associated with each edge, or its edges may be directed from one vertex to another called directed graph(b).

A weighted graph is defined as a special type of graph in which the edges are assigned some weights which represent cost, distance, and many other relative measuring units.

Graph representations

Graphs are used to represent many real-life applications: Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. For example, in Facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender, and locale

There are different ways to store graphs in a computer system. The data structure used depends on both the graph structure and the algorithm used for manipulating the graph. Theoretically one can distinguish between list and matrix structures but in concrete applications the best structure is often a combination of both. List structures are often preferred for sparse graphs as they have smaller memory requirements. Matrix structures on the other hand provide faster access for some applications but can consume huge amounts of memory.

Graphs can be represented in different ways, and the choice of representation depends on the specific requirements and the type of operations you need to perform. Here are three common representations of graphs 

Two main data structures for the representation of graphs are used in practice. The first is called an adjacency matrix, in which the rows and columns of a two-dimensional array represent source and destination vertices and entries in the array indicate whether an edge exists between the vertices.The second is an adjacency list, and is implemented by representing each node as a data structure that contains a list of all adjacent nodes. Adjacency lists are preferred for sparse graphs; otherwise, an adjacency matrix is a good choice.

Adjacency Matrix:

In an adjacency matrix, a 2D array is used to represent a graph.

The rows and columns of the matrix represent the vertices, and the presence or absence of an edge between two vertices is indicated by a 1 or 0, respectively.

For a weighted graph, the matrix may store the weights of the edges instead of 1s and 0s.

Example:

Best For:

    Checking if there is an edge between two vertices.

    Representing dense graphs where most pairs of vertices are connected.

    Constant time complexity for checking adjacency.

    Memory-efficient for small graphs.

Not Ideal For:

    Sparse graphs, where most pairs of vertices are not connected.

    Consuming a lot of memory for large sparse graphs.

Adjacency List:

In an adjacency list, each vertex maintains a list of its adjacent vertices.

This representation is often more space-efficient than an adjacency matrix, especially for sparse graphs.

For a weighted graph, each entry in the adjacency list can also store the weight of the corresponding edge.

An array of lists is used. The size of the array is equal to the number of vertices. Let the array be an array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. Following is the adjacency list representation of the above graph.

Best For:

    Representing sparse graphs where few pairs of vertices are connected.

    Easily iterating through all neighbors of a vertex.

    Memory efficiency for sparse graphs.

Not Ideal For:

    Checking adjacency between arbitrary vertices in constant time.

    Dense graphs, where the overhead of maintaining lists for each vertex might be excessive.

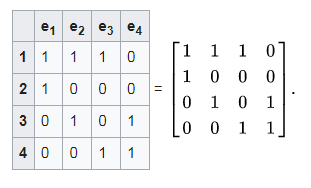
Incident Matrix

The incidence matrix is another way to represent a graph. In this representation, both vertices and edges of the graph are represented using a matrix. The matrix is often referred to as the "incidence matrix." Here's how it works:

Vertices and Edges Mapping:

Rows of the matrix represent vertices.

Columns of the matrix represent edges.

The element A[[i,j]] of A is 1 if the ith vertex is a vertex of the jth edge and 0 otherwise.(undirected graph)

The element A[[i,j]] of A is 1(outgoing) or -1(incoming if the ith vertex is a vertex of the jth edge and 0 otherwise.(directed graph)

For the weighted graph the entries represents the weight.

Best For

Network Flow Analysis
Linear Algebraic Techniques

Optimization Problems:They are beneficial in solving optimization problems related to graphs, particularly in scenarios where the emphasis is on edge properties.

Sparse Graphs:Incidence matrices: can be more memory-efficient than adjacency matrices for sparse graphs, where only a small fraction of the possible edges are present.

Not Best for

Graph Traversal:Incidence matrices are not as intuitive for graph traversal algorithms like Breadth-First Search (BFS) or Depth-First Search (DFS). Adjacency lists or matrices are typically more natural for these algorithms.

Checking Adjacency:If the primary operation involves checking whether two vertices are adjacent, incidence matrices are not the most efficient choice. Adjacency matrices or lists are better suited for such queries.

Dynamic Graphs:If the graph structure is frequently changing, updating the incidence matrix for dynamic graphs can be less efficient compared to other representations.

Memory Efficiency for Dense Graphs:For dense graphs where a large portion of the possible edges exists, the incidence matrix might not be as memory-efficient as an adjacency matrix.

C Implementation of adjacency matrix representation of a graph

C Implementation of adjacency list representation of a graph

C Implementation of incident matrix representation of a graph