Stack
A stack is a fundamental data structure in computer science and programming that follows the Last-In, First-Out (LIFO) principle. It is named "stack" because it resembles a stack of items, like a stack of plates or books, where you can only add or remove items from the top. Stacks are used for various purposes in programming and are essential in many algorithms and applications. Let's delve into the details of stacks:
Key Operations:
A stack typically supports two primary operations:
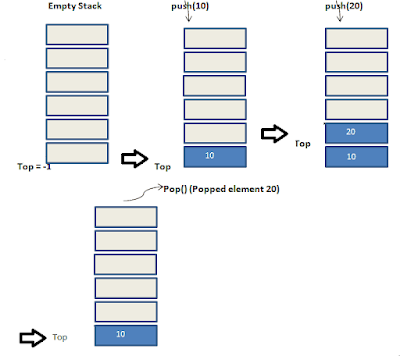
Push: This operation adds an element to the top of the stack. It is analogous to placing an item on top of the stack.
Pop: This operation removes and returns the top element of the stack. It is like taking the top item off the stack.
Additionally, stacks often provide the following operations:
Peek (or Top): This operation retrieves the top element without removing it. It allows you to examine the top item without modifying the stack.
IsEmpty: This operation checks if the stack is empty. If the stack has no elements, it returns true; otherwise, it returns false.
Properties of Stacks:
LIFO (Last-In, First-Out): The last element added to the stack is the first one to be removed. Think of it as a stack of plates; you take the top plate first.
Linear Data Structure: Stacks are linear data structures, meaning that they organize data in a straight line, unlike trees or graphs.
Limited Access: You can only directly access the top element of the stack. To access other elements, you must remove items from the top.
Implementation:
Stacks can be implemented using various data structures, such as arrays or linked lists. The choice of implementation depends on the specific requirements of your application.
Array-Based Stack: In this implementation, you use an array to store the elements of the stack. You keep track of the top element using an index or a pointer.
Linked List-Based Stack: Here, you use a linked list where each node contains an element and a reference (pointer) to the next node. The top of the stack is the head of the linked list.
Use Cases:(Applications)
Function Call Stack: Stacks are crucial in programming languages for managing function calls and maintaining the order of execution.
Expression Evaluation: Stacks are used to evaluate mathematical expressions, such as converting infix expressions to postfix (RPN) or solving equations.
Undo/Redo Functionality: Stacks are used to implement undo and redo functionality in applications like text editors.
Backtracking Algorithms: Stacks help in backtracking algorithms like depth-first search (DFS).
Complexity Analysis:
Push, Pop, Peek, and IsEmpty operations in a stack typically have a time complexity of O(1) when implemented using an array or linked list.
In summary, a stack is a simple yet powerful data structure that follows the Last-In, First-Out (LIFO) principle. It is widely used in computer science and programming for managing data and controlling the flow of execution in various applications. Understanding how to use stacks effectively is essential for any programmer or computer scientist.
Algorithms for stack operations
Initialize an array to store the stack elements
Initialize a variable top to -1 // Initialize an empty stack
Function Push(element):
1. If top is equal to the size of the array minus 1:
- Return an error or handle overflow (stack is full).
2. Increment top by 1.
3. Set array[top] to element.
Function Pop():
1. If top is equal to -1:
- Return an error or handle underflow (stack is empty).
2. Set element to array[top].
3. Decrement top by 1.
4. Return element.
Function Peek():
1. If top is equal to -1:
- Return an error or handle underflow (stack is empty).
2. Return array[top].
Function IsEmpty():
1. Return (top == -1).
Make sure to handle overflow (pushing elements onto a full stack) and underflow (popping or peeking from an empty stack) appropriately in your code to avoid errors and maintain the integrity of the stack.
Pseudo code for the Stack operations
// Initialize an empty stack
Initialize an array to store the stack elementsInitialize a variable top to -1
Function Push(element):
if top is equal to the size of the array minus 1:
// Stack is full, cannot push more elements
return an error or handle overflow
top = top + 1
array[top] = element
Function Pop():
if top is equal to -1:
// Stack is empty, cannot pop elements
return an error or handle underflow
element = array[top]
top = top - 1
return element
Function Peek():
if top is equal to -1:
// Stack is empty, cannot peek
return an error or handle underflow
return array[top]
Function IsEmpty():
if top==-1
return 1
else
return 0 // or use return (top == -1)
C- Program Stack Implementation
/*******************************************************************************/
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#define MAX_SIZE 100
// Global variables for the stack
int stack[MAX_SIZE];
int top = -1; // Initialize an empty stack
// Function to push an element onto the stack
void Push(int element) {
if (top == MAX_SIZE - 1) {
printf("Stack overflow: Cannot push element onto a full stack\n");
return; // Handle overflow (stack is full)
}
top++;
stack[top] = element;
}
// Function to pop an element from the stack
int Pop() {
if (top == -1) {
printf("Stack underflow: Cannot pop element from an empty stack\n");
return -1; // Handle underflow (stack is empty)
}
int element = stack[top];
top--;
return element;
}
// Function to peek at the top element of the stack
int Peek() {
if (top == -1) {
printf("Stack is empty Underflow!\n");
return -1; // Handle underflow (stack is empty)
}
return stack[top];
}
// Function to check if the stack is empty
bool IsEmpty() {
return (top == -1);
}
void Display()
{ int i;
if(IsEmpty()) printf("Stack is empty Under flow!\n");
else
{
printf("Stack contents are\n");
for(i=top;i>=0;i--)
printf("%d\n",stack[i]);
}
}
int main() {
int item, choice;
printf("\t\t\tImplementation Of Stack ");
do {
printf("\n\n1.Push\n2.Pop\n3.Peek\n4.Display\n5.exit\n");
printf("\nEnter Your Choice :: ");
scanf("%d", &choice);
switch (choice) {
case 1:
printf("\nEnter The item to be pushed :: ");
scanf("%d", &item);
Push(item);
break;
case 2:
if (IsEmpty())
printf("\nEmpty stack!Underflow !!");
else {
item = Pop();
printf("\nThe popped element is %d", item);
}
break;
case 3:
if (IsEmpty())
printf("\nEmpty stack!Underflow !!");
else {
item = Peek();
printf("\nThe Top element is %d", item);
}
break;
case 4:
Display();
break;
case 5:
exit(0);
}
} while (1);
return 0;
}
Write an algorithm to reverse a string using a stack.( University question)
Algorithm ReverseStringWithStack(input_string):
1. Create an empty stack of characters.
2. For each character, char, in input_string:
a. Push char onto the stack.
3. Create an empty string, reversed_string.
4. While the stack is not empty:
a. Pop a character, popped_char, from the stack.
b. Append popped_char to reversed_string.
5. Return reversed_string.
This algorithm uses a stack to reverse a given string. It iterates through each character in the input string, pushing them onto the stack. Then, it pops characters from the stack to construct the reversed string. The reversed string is the result of the algorithm.


Comments
Post a Comment